That models the road surface. Assume that the origin is at the center of the road.
Solution Roads Are Designed With Parabolic Surfaces To Allow Rain To Drain Off A Particular Road That Is 32 Quot Feet Wide Is 0 4 Foot Higher In The Center That It Is On
And determine How far from the center of the road is the road surface 02 feet.

. Roads are often designed with parabolic surfaces If subtlety isnt your point go for something with a little more bling. A particular road is 32 feet wide and 04 foot higher in the center than it is on the sides see figure. Roads are often designed with parabolic surfaces to allow rain to drain off.
Assume that the originis at the center of the road X2 -640. Find an equation of the parabola that models the road surface. A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides see.
A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides. Roads are often designed with parabolic surfaces to allow rain to drain off. Find the equation of the parabola that models the the road surface by assuming that the center of the parabola is at the origin.
Find the slope and change in elevation over a one-mile section of the road. Assume that the origin is at the center of the road. Ax2 bx c y.
Find an equation of the parabola that models the road surface. In order to allow rain to run off of a road they are often designed with parabolic surfaces in mind. A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides.
ROAD DESIGN Roads are often designed with parabolic surfaces to allow rain to drain off. A particular rond is 32 feet wide and 04 foot higher in the center than it is on the sides tee figure 04 a Write an equation of the parabola with its vertex at the origin that models the road surface. From terms to jewels as well as chains theres no Restrict towards the 3D factors it is possible to connect on your nails so get Inventive and let free.
A particular road is 32 feet wide and 04 foot higher in the center than it is on the sides see figure. ROAD DESIGN Roads are often designed with parabolic surfaces to allow rain to drain off. A particular road that is 44 feet wide is 04 foot higher in the center than it is on the sides see figure.
A particular road is that is 32 feet wide is 4 feet higher in in the center then on the sides. 32 ft 04 ft Nor draw to scale a Write an equation of the parabola with its vertex at the origin that models the road surface. A particular road is 32 feet wide and 04 foot higher in the center than it is on the sides see figure.
Roads are often designed with parabolic surfaces to allow rain to drain off. A particular road that is 32 feet wide is 04 foot in the center than it is on the sides. Roads are often designed with parabolic surfaces to allow rain to drain off.
Roads are often designed with parabolic surfaces to allow rain to drain off. Assume that the origin is at the center of the road. Civil engineers often design road surfaces with parabolic cross sections to provide water drainage.
Roads are often designed with parabolic surfaces to allow rain to drain off. U bris miss a wifi ist Jicho arti to nolteups na bril 2 In order to allow rain to run off of a road they are often designed with parabolic surfaces in mind. Roads are often designed with parabolic surfaces to allow to drain off.
I am struggling to get an equation of the parabola with its vertex at the origin. Write an equation of. That models the road surface.
Find an equation of the parabola with its vertex at the origin that models the road surface. Roads are often designed with parabolic surfaces to allow to drain off. In order to allow rain to run off of a road they are often designed with parabolic surfaces in mind.
Roads are often designed with parabolic surfaces to allow rain to drain off. Up to 24 cash back b Roads are often designe wi parabolic surfaces to allow for rain to drain off. A particular road that is 32 feet wide is 04 foot higher in the center that it is on the sides.
Roads Are Often Designed With Parabolic Surfaces. A Find an equation if the parabola that models the road surface. Suppose a road is 32 feet wide and 04 foot higher in the center than it is on the side.
Assume a road surface on level ground is 32 feet wide and is 04 foot higher at its center point than at its edges. Find an equation of the parabola with its vertex at the origin that models the road surface. A Find an equation of the parabola that models the road surface.
See figure a Find an equation of the parabola with its vertex at. A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides see figure. A particular road is 32 feet wide and 04 feet higher in the center than it is on the sides see figure.
Road Design Roads are often designed with parabolic surfaces to allow rain to drain off. A Develop an equation of the parabola with its vertex at the origin. Road Design Roads are often designed with parabolic surfaces to allow rain to drain off.
That models the road surface. Assume that the origin is at the center of the road a. A particular roads 32 feet wide and 04 foot higher in the center than it is on the sides see figure 041 Wine an equation of the parabola with its vertex at the origin that models the road surface Assume that the origin is at the center of the road.
Roads are often designed with parabolic surfaces to allow rain to drain off. Suppose a road is 32 feet wide and 04 foot higher in the center than it is on the side. Roads are often designed with parabolic surfaces to allow rain to drain off.
Roads are designed with parabolic surfaces to allow rain to drain off. A Find an equation of the parabola that models the road surface. Find the equation using the form.
Roads are often designed with parabolic surfaces to allow to drain off. A particular road is 32 feet wide is 04 foot highter in the center than it is on the sides Glb-qò a Find an equation if the parabola with its vertex at the origin that models the road surface pc-Ibo b How far from the center of the road is the road surface. A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides see figure.
Roads are designed with parabolic surfaces to allow rain to drain off. Suppose a road is 32 feet wide and 04 foot higher in the center than it is on the side a. A particular road that is 32 feet wide is 04 foot higher in the center than it is on the sides.

Solved Roads Are Often Designed With Parabolic Surfaces To Chegg Com

Solved 64 Road Design Roa D Are Often Deslgned W Th Parabolic Surfaces Toallow Rain Tdrarn Off 0parhcular Rad Is 32 Feetwide And 0 4 Foot Higher 10 The Center Than Ts On The Sudes Q Ucile An
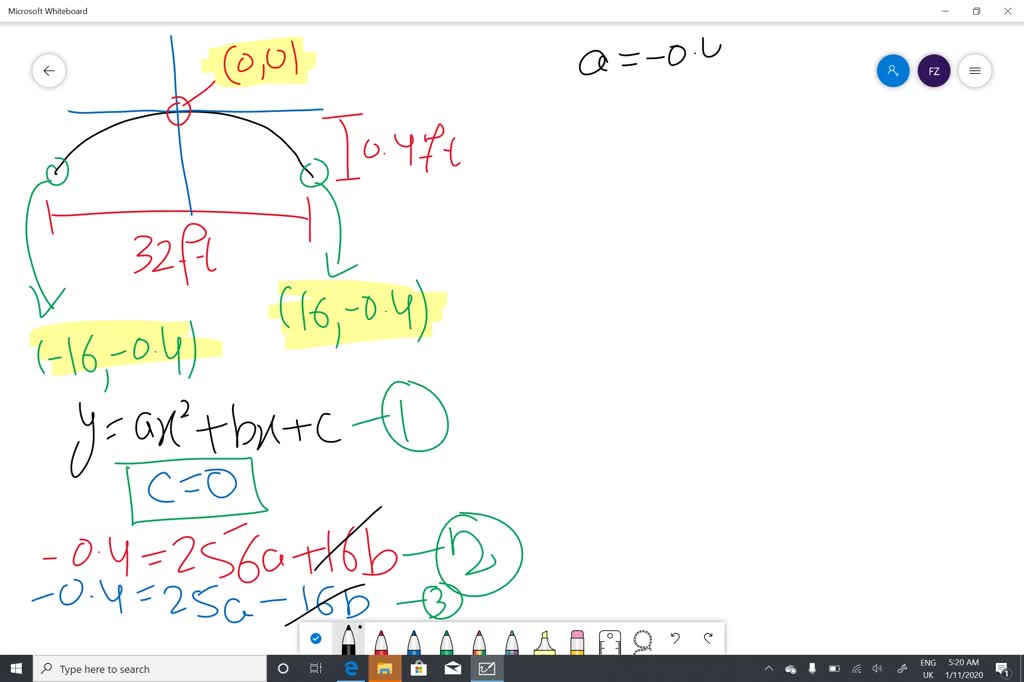
Solved Road Design Roads Are Often Designed With Parabolic Surfaces To Allow Rain To Drain Off A Particular Road That Is 32 Feet Wide Is 0 4 Foot Higher In The Center Than It

Solved 7 Roads Are Often Designed With Parabolic Surfaces Chegg Com
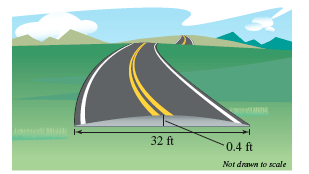
Solved Roads Are Often Designed With Parabolic Surfaces To Chegg Com
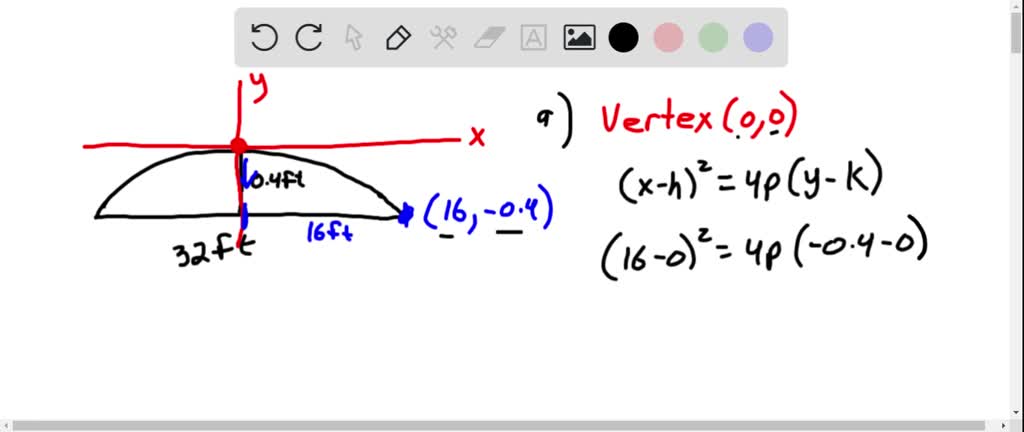
Solved Road Design Roads Are Often Designed With Parabolic Surfaces To Allow Rain To Drain Off A Particular Road That Is 32 Feet Wide Is 0 4 Foot Higher In The Center Than It

Solved Roads Are Often Designed With Parabolic Surfaces To Chegg Com
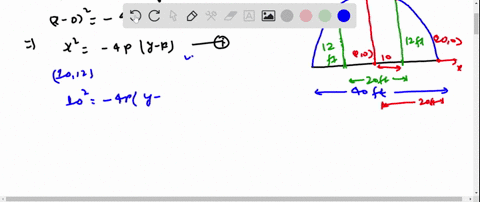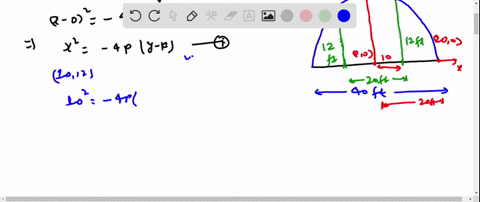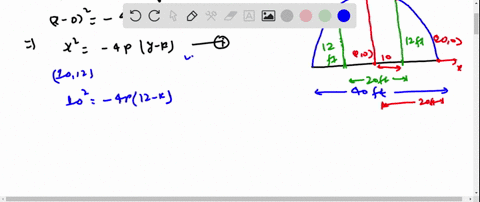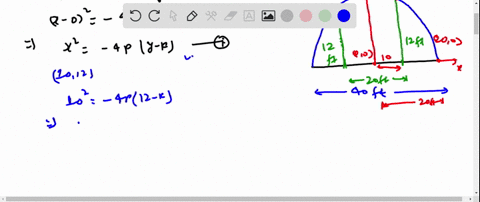
Solved Road Design Roads Are Often Designed With Parabolic Surfaces To Allow Rain To Drain Off A Particular Road That Is 32 Feet Wide Is 0 4 Foot Higher In The Center Than It
0 comments
Post a Comment